Ever wondered what makes steel such a vital material in engineering and construction? The answer lies in its remarkable mechanical properties, particularly its elasticity. Young’s modulus, a fundamental measure of a material’s stiffness, plays a crucial role in determining how steel responds to stress and strain.
But what exactly is Young’s modulus, and why is it so important for steel? This article delves into the definition, typical values, and methods of calculating Young’s modulus for steel.
Additionally, we’ll explore its practical applications in various industries and examine how factors like temperature and composition influence this key property. Ready to uncover the secrets behind steel’s incredible strength and flexibility? Let’s dive in.
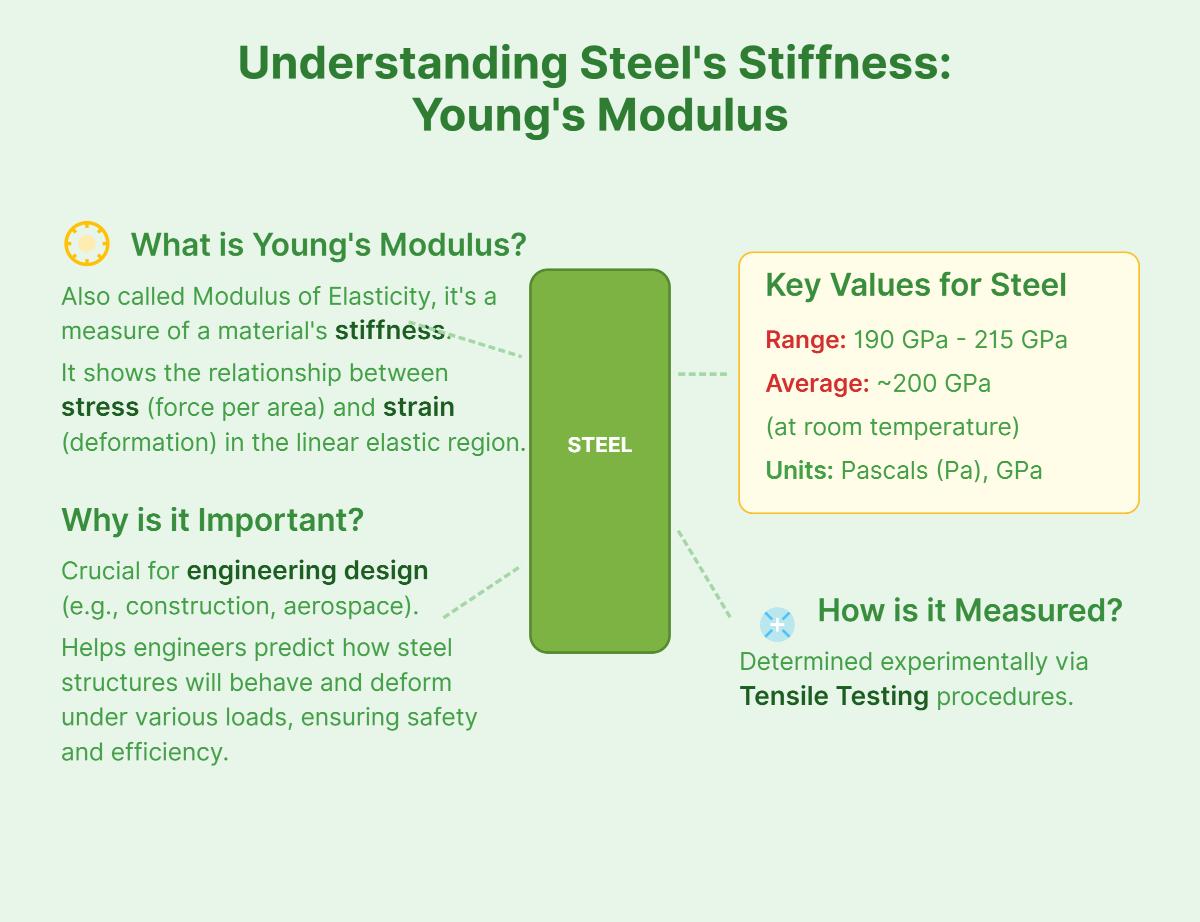
Young’s modulus, also known as the modulus of elasticity, measures the stiffness of a material. It quantifies how a material resists deformation under stress and returns to its original shape once the stress is removed. This property is essential for understanding the elastic behavior of materials within their elastic limits.
To grasp Young’s modulus, one must understand stress and strain. Stress is the force applied per unit area of the material, while strain is the deformation experienced by the material, expressed as the change in length divided by the original length. Stress is measured in pascals (Pa), and strain is a dimensionless quantity.
Young’s modulus (E) is calculated by dividing stress (σ) by strain (ε):
E=σ/ε
This formula highlights that Young’s modulus is the slope of the stress-strain curve in the elastic region of the material.
Young’s modulus is crucial for predicting material behavior, comparing materials, and ensuring quality control. It allows engineers to determine how materials will respond to various loads, aiding in the selection of appropriate materials for specific applications.
Young’s modulus applies only within the elastic deformation range:
Understanding these deformation types is crucial for ensuring materials are used within their safe limits.
For steel, Young’s modulus typically ranges from 200 to 210 GPa (gigapascals), indicating its high stiffness and suitability for load-bearing applications. This property is integral to designing and analyzing steel structures to ensure they withstand required loads without excessive deformation.
Knowing Young’s modulus helps engineers design components that maintain their shape under load, such as beams and mechanical parts. This understanding is essential for creating structures and mechanisms that are both efficient and reliable.
Young’s modulus, a measure of stiffness, is typically expressed in pressure units like Pascals (Pa), Megapascals (MPa), or Gigapascals (GPa).
In the Imperial system, the units used are:
These units standardize measurements, ensuring consistent communication of material properties across different regions and industries.
The Young’s modulus of steel typically falls within a specific range, reflecting its high stiffness and suitability for structural applications. The standard value is approximately 200 GPa (29,000,000 psi). However, depending on the specific type and composition of the steel, this value can vary slightly:
These values indicate that steel is a very stiff material, capable of withstanding significant stress with minimal deformation.
As temperature rises, steel becomes less stiff, reducing its Young’s modulus. For instance, at 200°C, it drops to about 193 GPa, and at 490°C, it falls to around 152 GPa. This temperature dependence is crucial for applications involving high temperatures, such as in power plants or industrial furnaces.
Different alloy compositions can also affect Young’s modulus. Carbon steels generally have a Young’s modulus of 200-210 GPa, while stainless steels, which include chromium and nickel, range from 190-200 GPa. Understanding these variations is essential for selecting the right type of steel for specific engineering applications, ensuring optimal performance and safety.
Understanding Young’s modulus is crucial for engineers. It helps in structural analysis, material selection, and design optimization, ensuring structures withstand stress without deforming. Knowing the precise value of Young’s modulus for a given type of steel aids in:
In summary, the values and units of Young’s modulus are foundational for material science and engineering, providing critical data for designing and analyzing steel structures and components.
Young’s Modulus is a fundamental property of materials that describes their stiffness. It is crucial in understanding how materials like steel deform under stress, which is essential in construction and manufacturing. By determining Young’s Modulus, engineers can predict how much a material will stretch or compress under a given load.
Consider a steel sample with:
Using the formula:
E=(1000N×2m)/(0.0001m2×0.04m)=5×108Pa.
In real-world applications, such as in construction, knowing the Young’s Modulus helps in designing structures that can withstand specific loads without excessive deformation, ensuring safety and stability.
To calculate Young’s Modulus using a stress-strain curve:
Several tools and software can assist in calculating Young’s Modulus:
These tools are widely used in industries to ensure materials meet specific standards and perform reliably under expected loads. By understanding and utilizing these tools, engineers can design more efficient and safer structures.
Young’s Modulus is essential for guaranteeing the stability and durability of structures like buildings and bridges. Engineers use it to calculate how much a structure will deform under various loads, which is vital for designing components that can withstand stress without failure, ensuring that structures maintain their integrity and safety over time. This modulus aids in selecting the appropriate type of steel to meet the mechanical demands of different structural elements.
In mechanical engineering, Young’s Modulus is used to analyze and design machinery and mechanical systems. Understanding the modulus helps optimize the performance and lifespan of components in various applications, from industrial machinery to consumer products. It is crucial for designing engines, machines, and equipment that operate reliably under mechanical stress.
In the automotive industry, the stiffness of steel, as indicated by Young’s Modulus, is vital for designing vehicle components such as chassis, suspension systems, and engine parts. Engineers use the modulus to design components that balance strength and flexibility, enhancing vehicle durability and efficiency. This balance contributes significantly to the overall performance and safety of vehicles.
Aerospace engineering requires materials that offer high strength-to-weight ratios and reliability under extreme conditions. Young’s Modulus is critical for designing aircraft and spacecraft components, where precise calculations of deformation under stress are necessary. This ensures that materials meet the stringent performance standards required for aerospace applications, enabling safe and efficient operation.
In civil engineering, Young’s Modulus is used to evaluate the behavior of steel in construction materials like beams, columns, and reinforced concrete. Civil engineers rely on this modulus to predict how these materials will perform under various loads, ensuring that infrastructure projects are safe and sustainable. It is particularly important in seismic design, where understanding material deformation can help mitigate earthquake damage.
Young’s Modulus assists in selecting the appropriate type of steel for different applications by providing insights into the material’s stiffness and elasticity. This is crucial for ensuring the chosen steel meets the project’s specific mechanical requirements. Engineers can make informed decisions about material selection, balancing cost, performance, and safety.
The temperature dependence of Young’s Modulus is a key consideration in industries where steel is exposed to varying environmental conditions. Applications such as power plants and industrial furnaces require materials that perform consistently across a range of temperatures. Understanding how Young’s Modulus varies with temperature helps in designing components that maintain their integrity and function effectively under thermal stress.
As steel heats up, its stiffness, indicated by Young’s modulus, tends to decline. This phenomenon occurs due to the heightened thermal vibrations of the atoms within the material. Heating steel intensifies atomic vibrations, weakening bonds and reducing stiffness, which lowers Young’s modulus.
Higher temperatures increase atomic vibrations in steel, causing bonds to weaken and reducing stiffness. This effect is less pronounced in metals compared to polymers, but still significant. The increased atomic movement reduces the effectiveness of the bonds holding the material together, thereby lowering Young’s modulus.
The relationship between Young’s modulus and temperature is also influenced by the coefficient of thermal expansion. As steel’s temperature rises, its coefficient of thermal expansion increases, further contributing to the reduction in Young’s modulus. This means that the material expands more with increasing temperature, which exacerbates the weakening of atomic bonds and the overall decrease in stiffness.
At elevated temperatures, the behavior of steel changes in several ways. The decrease in Young’s modulus can be partially offset by an increase in the number of dislocations within the crystal structure of the material. These dislocations allow atoms to move more easily, making the material more ductile at higher temperatures even as its stiffness decreases. This ductility is beneficial in certain applications where flexibility is required to prevent brittle failure.
Knowing how Young’s modulus changes with temperature is vital for designing steel components in high-heat environments like power plants and industrial furnaces. Engineers must consider this to ensure structural integrity and performance. They need to account for the gradual reduction in Young’s modulus with increasing temperature to ensure the components will function safely and effectively under operating conditions.
Young’s Modulus is essential for choosing materials, especially when stiffness and load-bearing strength are needed. It measures a material’s resistance to deformation under stress, which is crucial in preventing structural failure in buildings, bridges, and other infrastructures.
When selecting materials for engineering projects, several criteria are considered, including:
Young’s Modulus affects how materials behave under different loads. Knowing this helps engineers predict how much a structure will bend or stretch, ensuring it remains safe and durable.
In structural design, calculating deflection and stress is essential for assessing the integrity and performance of materials. Young’s Modulus enables engineers to:
In construction, steel’s high Young’s Modulus makes it an ideal choice for load-bearing structures. Its ability to resist deformation under heavy loads ensures that buildings, bridges, and other infrastructures remain stable and secure. Engineers use steel for its predictable behavior and reliability in supporting significant weights.
Automotive components must endure dynamic stresses and vibrations while maintaining precise dimensions and performance. Young’s Modulus helps in designing parts that are both strong and lightweight, ensuring vehicle durability and efficiency. Steel’s stiffness contributes to the structural integrity of the vehicle, providing the necessary strength to withstand impacts and maintain shape under various loads.
In aerospace applications, materials must maintain structural integrity under extreme conditions. Young’s Modulus is crucial for selecting materials that can withstand high stresses and temperatures encountered during flight. Steel, with its high modulus, provides the necessary stiffness and strength for critical components, ensuring the safety and reliability of aircraft.
While Young’s Modulus is a fundamental property for material selection and structural design, engineers must also consider:
Below are answers to some frequently asked questions:
Young’s modulus of steel, also known as the modulus of elasticity, is a measure of the material’s stiffness, indicating the relationship between stress and strain within its linear elastic region. At room temperature, it typically ranges from 190 GPa to 215 GPa, with an average value around 200 GPa. This property is crucial for engineering applications, such as construction and aerospace, as it helps predict how steel will behave under various loads. Young’s modulus is measured in Pascals (Pa) or its multiples, and is determined through tensile testing, as discussed earlier in the article.
As temperature increases, the Young’s modulus of steel decreases due to heightened atomic vibrations that weaken interatomic bonds, leading to reduced stiffness. At room temperature, it typically ranges from 190 GPa to 215 GPa, but can drop to about 150 GPa at 600°C. This temperature-dependent change is consistent across different steel types, regardless of alloy composition. Understanding this effect is crucial in engineering applications where steel is exposed to high temperatures, ensuring that materials maintain integrity and performance under varying thermal conditions. Testing methods like tensile testing and flexural vibration tests help measure these changes.
Young’s modulus of steel is widely used in engineering for structural design and analysis, material selection, finite element analysis, fatigue testing, and dynamic behavior studies. It helps engineers predict deformation under various loads, choose appropriate materials, model elastic properties in simulations, evaluate long-term durability, and design structures to withstand dynamic loads. Additionally, it aids in optimizing material usage in manufacturing processes, ensuring cost-effective and sustainable solutions. Overall, understanding Young’s modulus is essential for ensuring the performance, safety, and durability of steel structures in engineering applications.
Young’s modulus is calculated by determining the ratio of stress to strain within the elastic region of a material. For steel, this involves applying a known force (F) to a sample with a defined cross-sectional area (A) and measuring the resulting change in length (ΔL). Stress is calculated as (F/A), and strain as (ΔL/L), where (L) is the original length. The modulus (E) is then (E=σ/ϵ). This calculation assumes the material remains elastic and undamaged. For steel, typical values are around 200 GPa, illustrating its high stiffness and resistance to deformation.
Young’s Modulus of steel is crucial in various real-world applications, such as the design and analysis of structures like buildings and bridges, where it helps determine the load-carrying capacity and deformation. It’s also vital in material selection for automotive and aerospace components that require high stiffness, fatigue testing for durability, and the construction of resilient bridges. Additionally, it plays a significant role in understanding vibrations and dynamic behavior in structures, ensuring they can withstand dynamic loads and vibrations without failing. These applications illustrate the importance of Young’s Modulus in ensuring structural integrity and performance.
Young’s modulus is measured in various units depending on the system used. In the International System of Units (SI), it is primarily expressed in pascals (Pa), but due to its large values, it is more commonly represented in gigapascals (GPa). In the U.S. Customary system, it is often measured in pounds per square inch (psi) or kilopounds per square inch (ksi). Other units like newtons per square meter (N/m²) or newtons per square millimeter (N/mm²) can also be used, though they are less common. For steel, typical values are around 190-210 GPa or 27500-31200 ksi.
Young’s Modulus, also known as the modulus of elasticity, is crucial in material selection because it measures the stiffness of a material, indicating how much it resists deformation under stress. This property is vital for ensuring that materials used in engineering applications can withstand the forces they will encounter without excessive deformation. For instance, in the construction of buildings and bridges, materials with a high Young’s Modulus, like steel, are preferred because they offer the necessary rigidity and strength to support heavy loads. Additionally, in mechanical components such as springs and beams, Young’s Modulus helps determine the material’s deformation under load, ensuring performance and reliability. In industries like aerospace and automotive, it balances stiffness and flexibility in components, maintaining structural integrity under varying stresses. Thus, Young’s Modulus is fundamental in selecting materials that meet specific mechanical and performance criteria, ensuring safety, efficiency, and cost-effectiveness in various engineering applications.

